

For example, we would perhaps like to have three different sensitivities: a) on changes of short term rates, b) on changes of medium term rates and c) on changes of long term rates. What we need is not a single measure of how sensitive our bond is on generic yield changes, but rather several different measures that quantify our bond's sensitivity on various maturity regimes. Certain market events may lead to a spike of the short term interest rates or credit spreads (both are relevant to the bond's yield) but cause no change on the long term rates and spreads. It is a fact that bond price changes are not uniform over the maturity spectrum. Quite often, we are interested in how a bond price reacts on price changes of certain benchmark highly liquid bonds - such as treasury bonds - of various maturities. While – as explained – the first assumption is perhaps unrealistic but not bad since it still produces the correct current bond price, the second assumption is practically useful only if we are interested in calculating the sensitivity of the bond price with regard to a change of its own yield. Beyond that, y cannot be applied to any other bond, not even to compute the present value of a single isolated cash flow of the same bond.Īssumption 2: The new bond price is calculated under the assumption that the theoretical flat yield y applicable to each cash flow C i changes by the same amount Δy (discrete or infinitesimal), regardless of the time T i. Take the bond away and you discover that y has no real world connection to each maturity T i in isolation! The only value of y is that it does its job well with respect to its linked bond, namely calculating the bond's present value. Note here that y is a purely theoretical interest rate linked to our particular bond (stream of cash flows), defined so that the cumulative present value of all cash flows equals the observed bond's dirty price. Now that we have refreshed our memory with the details of the Modified Duration, we notice that the present values of all cash flows are recomputed based on two highly unrealistic assumptions:Īssumption 1: Applicable for the discounting of each cash flow C i is the same flat yield y, regardless of the time T i on which the C i is paid.

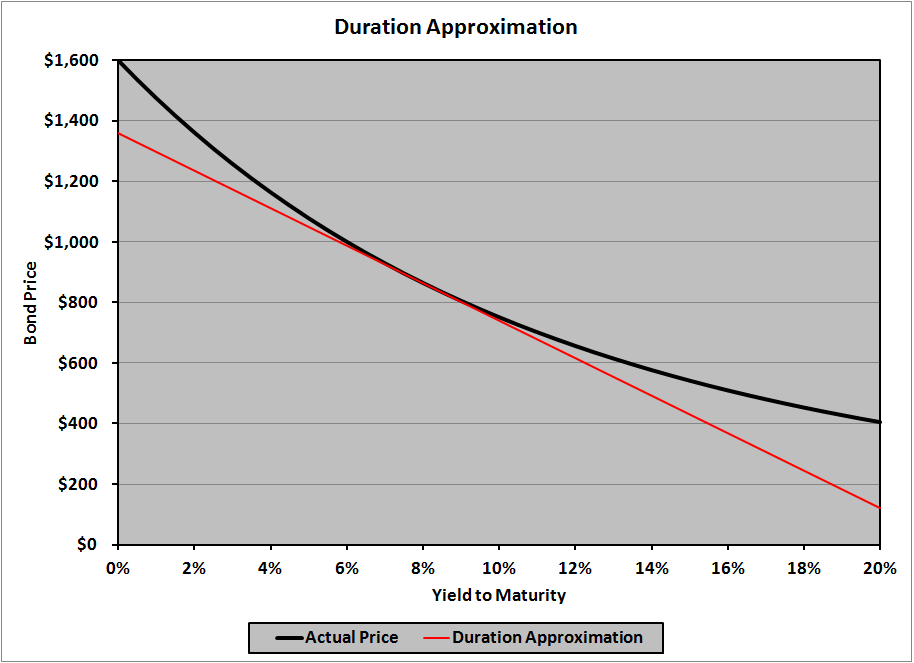
The advantage of this approach is that one discounting operation - rather than two - suffices for calculating the symmetric two-sided derivative that is needed by the definition of the Modified Duration. For example, if y is defined with the continuous compounding convention, then its associated discount factor that applies to the i th cash flow C i paid at time T imust equal e -yTi, meaning that Bi = e -yTiC i and therefore:ĭB i/ dy = d(e -yTiC i)/ dy = -C iT i e -yTi Now each derivative can be easily calculated provided we know how the yield y is defined. Since a derivative acts linearly on a sum, it follows: Then rather than calculating the theoretical bond prices corresponding to shifted yields, QuantLib regards B as the sum B 1+B 2+…B n of the present values of the bond's cash flows B 1, B 2, …, B n. Then they form the dirty bond price difference ΔB = B +-B - and plug everything in the formula to get:įree and open source QuantLib calculates the Modified Duration of fixed rate bonds analytically by setting Δy -> 0, which transforms the definition formula to one involving the derivative dB/ dy of B with respect to y: More specifically, most practitioners take Δy in the above formula to mean the difference y +-y - = 2 δ, where y + = y+ δ and y - = y- δ and δ is the absolute one-sided yield shift, typically 1%. The actual practice follows a slightly different interpretation of the above formula so that both the upside and downside yield movements are considered in a symmetrical fashion. Finally they would calculate the difference ΔB = B ΄-B and then the Duration D from the formula above. For example, they would shift an initial yield of y = 5% to y ΄ = y+ Δy = 5% + 1% = 6% and then they would calculate the theoretical bond price B ΄ implied by the shifted yield y ΄. There is still some residual uncertainty in this definition due to the yet unspecified size of the assumed yield change Δy. While there exist several different Duration definitions that produce slightly different results, the one that is most closely related to the Key Rate Duration is the Modified Duration D, which may be defined in a very general fashion with respect to any stream of future cash flows as the negative of the relative change - ΔB/B of a bond's initial dirty price B caused by a change Δy in its initial yield y, divided by that change Δy. You are all familiar with the concept of bond Duration, which tells us how much a bond's price changes if its yield goes up or down by a small amount.


 0 kommentar(er)
0 kommentar(er)
